Les actions et les valeurs à risque – notions de gestion de portefeuille – II
Pourquoi diversifier le portefeuille de placement
Le premier article de cette série, publié en novembre dernier, a présenté différentes techniques pour diversifier le portefeuille de placement. Dans ce deuxième article nous traitons de la justification théorique de cette stratégie. Intuitivement, on accepte d’emblée qu’il ne faut pas mettre tous ses œufs dans le même panier. Alors pourquoi, vous demanderez-vous peut-être, est-il utile d’en faire la démonstration théorique ? Les gestionnaires professionnels s’intéressent à cette démonstration parce qu’elle leur permet de mieux comprendre ce qu’est la diversification et ce qui constitue une bonne diversification du portefeuille. Même lorsqu’il n’envisage pas mettre en pratique lui-même les techniques qui découlent de ces connaissances, l’investisseur particulier a tout avantage à en comprendre les principaux fondements.
Combien faut-il de titres différents pour réduire suffisamment le risque ?
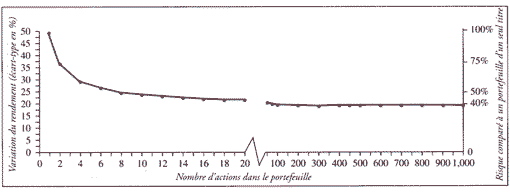
Quant il s’agit des valeurs à risque, les spécialistes de la finance font la distinction entre deux types de risque, le risque lié au marché et le risque spécifique. Le risque lié au marché est le risque que le prix de certaines valeurs à risque, par exemple celles de votre portefeuille, fluctuent à hausse ou à la baisse en synchronisme avec la tendance générale des marchés de valeurs de placement. Le risque spécifique, aussi appelé risque non systématique est décrit dans le Dictionnaire de la comptabilité comme «la partie du risque d’un titre qui est spécifiquement attribuable à ce titre et qui, par conséquent, peut être éliminé par la diversification du portefeuille de titres»1. Dans un article célèbre, Meir Statman s’est intéressé à la question de savoir combien de titres devrait contenir un portefeuille pour qu’on observe une réduction appréciable du risque spécifique2. Le résultat de cette recherche est présenté à la figure 1.
1 Ménard L., Dictionnaire de la comptabilité et de la gestion financière, ICCA, 1994
2 Statman M., How Many Stocks Make a Diversified Portfolio, Journal of Financial and Quantitative Analysis, septembre 1987
Ce que nous dit cette illustration, c’est qu’un portefeuille qui contiendrait 1000 titres à risque choisis au hasard aurait un risque global de 60% inférieur à celui d’un portefeuille composé d’un seul titre. Ce portefeuille n’exposerait alors son détenteur qu’au seul risque lié au marché puisque tout le risque spécifique y aurait été éliminé par la diversification. On y constate également, et c’est là une contribution majeure de Statman, qu’un portefeuille qui ne comporterait que 20 titres représentatifs du marché procure déjà l’essentiel des bénéfices qu’il y à retirer de la diversification du portefeuille de valeurs à risque. Un gestionnaire peut donc réduire de façon très importante le risque du portefeuille sans encourir de coûts d’administration excessifs pour effectuer les analyses et les transactions que cela requiert.
Améliorer le rapport rendement-risque en combinant des valeurs présentant différents degrés de risque
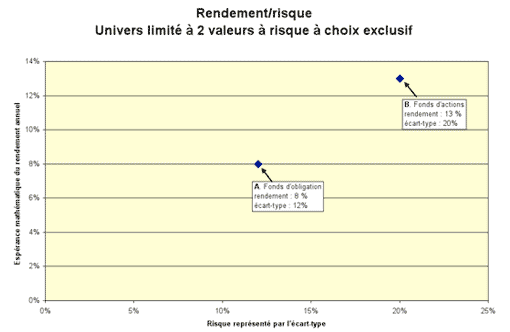
Les travaux de Harry Markovitz, un économiste de l’Université de Californie à qui on a décerné le Nobel d’économie en 1990, ont mené à une découverte majeure : un investisseur peut obtenir un meilleur rendement pour le même niveau de risque s’il détient un portefeuille bien diversifié, soit des titres présentant différents niveaux de risque. Pour illustrer cette affirmation, supposons un investisseur à qui s’offrent 2 choix d’investissements : a) un fonds d’obligation qui procure un rendement moyen de 8 % et un niveau de risque de 12 %, le fonds A, et b) un fonds d’actions dont le rendement moyen est de 13 % et le niveau de risque 20 % , le fonds B.
3 On a mesuré le risque avec l’écart-type, soit la différence moyenne entre le rendement d’une année quelconque et le rendement moyen. Pour le fonds d’obligation, un écart-type de 12 % signifie que les observations de rendement se trouveront entre -4 % et 20 % (8 % ± 12 %) avec une fréquence de 64 %, si on suppose que le rendement suit la distribution normale.
Si on suppose d’abord qu’un investisseur doit absolument choisir un ou l’autre de ces placements, les deux points tracés à la figure 2 représentent les seuls choix qui s’offrent à lui pour gérer le rapport rendement risque. Lorsqu’on introduit la possibilité de choix non-exclusifs, l’investisseur acquiert la possibilité de combiner les fonds A et B, ce qui augmente considérablement son éventail de choix en matière rendement-risque. Par exemple, il peut former un portefeuille contenant des parts égales du fonds A et du fonds B. Un tel portefeuille offre un espérance mathématique de rendement de 10,5 % (50 % de 8 % plus 50 % de 13 %), mais peut-on dire que son niveau de risque est de 16 %, soit la moyenne des taux de risque des deux fonds constituants ? La réponse est que le risque de ce portefeuille sera de 16 % seulement si les rendements des deux fonds sont parfaitement corrélés, ce qui signifie que le coefficient de corrélation (r) des rendements devra être égal à 1. Le coefficient de corrélation peut prendre des valeurs entre -1 et 1. La figure 3 montre l’éventail des choix rendement-risque d’un investisseur qui peut combiner les fonds A et B, selon que le coefficient de corrélation s’établit à -1, 0, 0,3 ou 1.
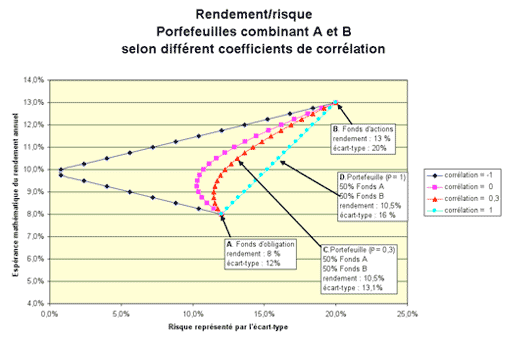
On observe que pour un coefficient de corrélation de 1, l’éventail des choix est représenté par une ligne droite qui relie A et B, mais que pour les autres valeurs du coefficients de corrélation, l’éventail des choix forme des courbes qui se retrouvent toutes au-dessus de la droite. Cela signifie que les portefeuilles que l’on obtient lorsque la corrélation entre les valeurs à risques est moins que parfaitement positive permettent d’améliorer le rapport rendement-risque, soit d’obtenir un rendement recherché à moindre risque. Par exemple, le point C sur le graphique nous montre un portefeuille formé à parts égales d’unités des fonds A et B, lorsque le coefficient de corrélation correspond à 0,3. Ce portefeuille génère un rendement de 10,5 %, comme le portefeuille D, mais son niveau de risque mesuré par l’écart-type n’est que de 13,1 %. Le cas limite des avantages que confère la diversification est atteint lorsque la corrélation entre les 2 fonds est parfaitement négative (-1). En fait, dans un tel cas, il est théoriquement possible, en dosant adéquatement A et B, de ramener le risque à 0 %.
Les études empiriques ont démontrés que les portefeuilles obtenus aléatoirement en combinant des valeurs de risques différents sont constitués de valeurs faiblement corrélées entre elles. De plus, les gestionnaires de portefeuilles qui veulent améliorer le rapport rendement-risque de leurs portefeuilles mettent un soin particulier à ne pas y inclure trop de valeurs qui présentent un haut degré de corrélation positive entre elles. Cette façon de faire est conforme à ce que les travaux de Markovitz ont révélé sur les avantages de la diversification : un portefeuille bien diversifié, qui inclut un bon éventail de valeurs présentant des degrés de risque différents, permet non seulement de réduire le risque, mais aussi d’obtenir un meilleur rendement pour un même niveau de risque.
Les deux premiers articles de cette série ont traité du comment et du pourquoi de la diversification du portefeuille. Le prochain article, qui sera publié au printemps, présentera une méthode d’évaluation facilitant la gestion du rapport rendement-risque du portefeuille. D’ici là, nos conseillers sont à votre disposition pour recueillir vos commentaires ou répondre à vos questions. N’hésitez pas à prendre contact avec eux.







